ENH: wallDistAddressing: wall distance which stores addressing.

Summary

In some physical models the distance-to-the-nearest-wall is used which involves calculating the nearest wall face. Some models additionally use the normal at that nearest wall face ('reflection vector') or even non-geometry data (e.g. y+ in the vanDriest LES delta model).

The normal algorithm uses the same method (meshWave) to transport both the originating face centre (to decide on the nearest) and any additional properties (normal, y+). The problem with this method is that any field-dependent data (e.g. y+) needs to go through the whole algorithm even though the geometry stays constant.

In this merge request there is a new wall distance calculation method which transports the originating face centres and addressing. This addressing can then be stored and used to get any value onto the internal field.

As a test the pipeCyclic tutorial case was modified. In the figures below black is the original geometry with a rotational cyclic from left to right. Orange is the original geometry transformed by 90 degrees to show the effect of the rotation. Pink is a new set of wall baffles (these are the only wall faces). The green lines are from the cell centres to the nearest wall. As can be seen the cells close to the left of the original geometry find their nearest on the transformed geometry.

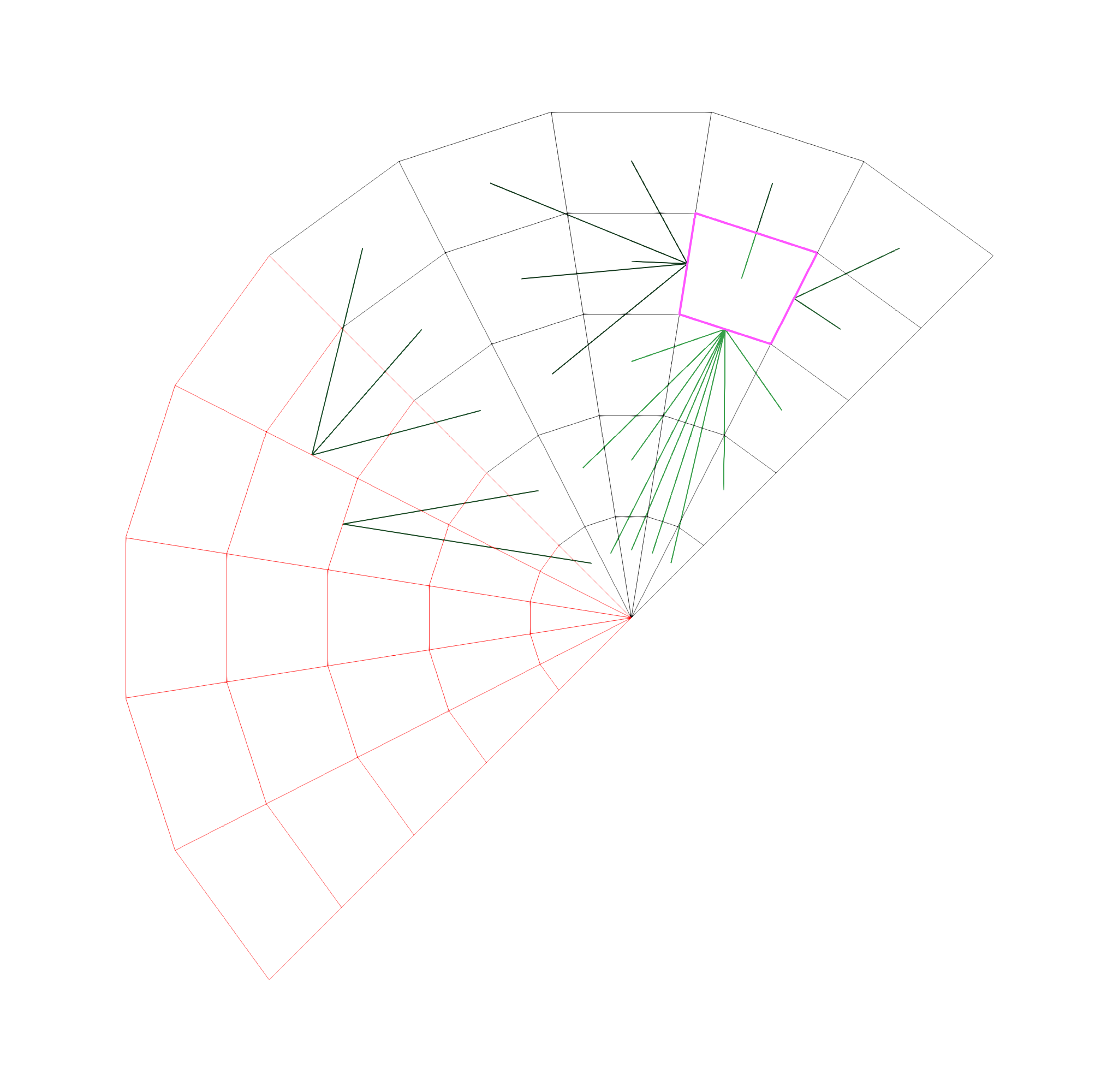
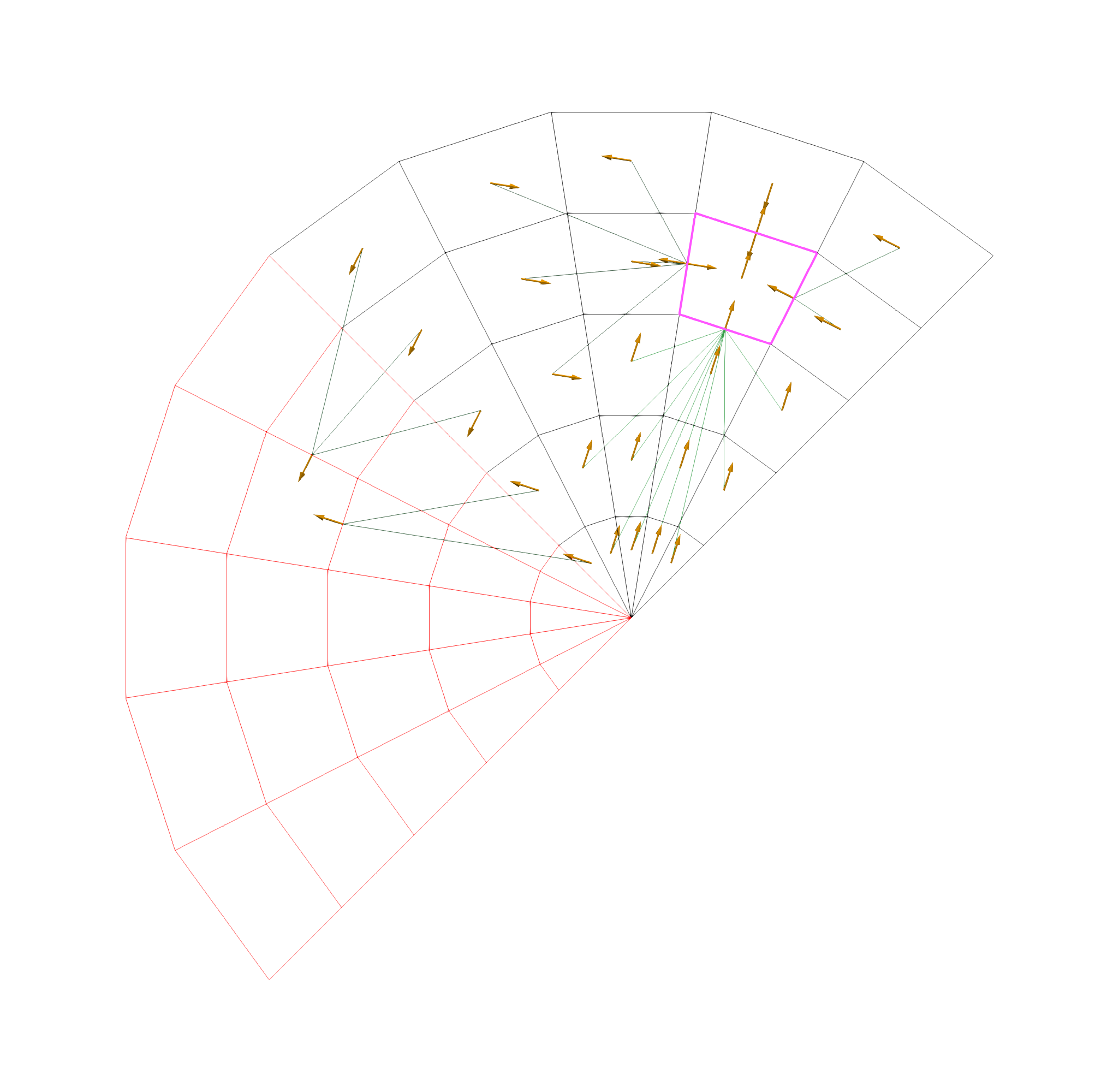
Similar, visualising the normals shows that it takes the corresponding normals of the rotated geometry

Resolved bugs (If applicable)

#2648 (closed)

Details of new models (If applicable)

• wallDistAddressing::New instead of wallDist::New
• stores distance y() and addressing (including transformations)
• contains helper functions to map data on selected patches onto internal field
• requires !589 (merged) to have named MeshObjects (if e.g. distance to non-wall patches is to be stored)
• used in vanDriest LESdelta
• used in meshWaveAddressing wall-distance calculation. In system/fvSchemes:

    wallDist
    {
        method          meshWaveAddressing;
        nRequired       true;
    }

• debugging : set DebugSwitches for wallDistAddressing:
  • 1 : report number of untransformed and transformed wall faces
  • 2 : dump nearest.obj file with lines/normals to/from nearest wall face

Risks

• slightly different behaviour at y+ 500. Before it would never visit cells surrounded by cells with y+ 500. In this version it calculates y+ everywhere and truncates afterwards. In tests we have not seen any difference.
• requires additional storage for transformations (sized with the number of wall faces and number of transformations)
• transformation support is only tested for a single transformation